Задача
Дано N точек, никакие три из которых не лежат на одной прямой. Каждые две из этих точек соединены отрезком, и каждый отрезок окрашен в один из k цветов. Докажите, что если N > [k!e], то среди данных точек можно выбрать такие три, что все стороны образованного ими треугольника будут окрашены в один цвет.
Решение
Индукция по k. База (k = 1) очевидна.
Шаг индукции. Как видно из задачи 160873 б),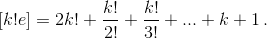 
Рассмотрим произвольную из N данных точек. Из неё выходит не менее 
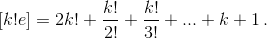отрезков, окрашенных в один и тот же цвет. Если концы каких-либо двух из этих отрезков соединены отрезком того же цвета, то нужный треугольник найден. В противном случае, концы соединяются отрезками, окрашенными в
k – 1 цвет. Согласно предположению индукции можно найти треугольник одного цвета с вершинами в этих точках.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь