Задача
Число e определяется равенством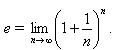 
Докажите, что а) 
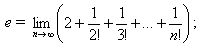б)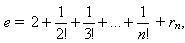 
где 0 < rn ≤ 1/n!n;в) e – иррациональное число.
Решение
а) Положим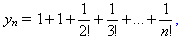 
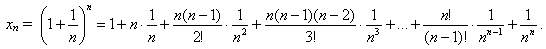
Достаточно доказать, что xn < yn ≤ e при n > 2. Левое неравенство очевидно, так как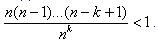 
Для доказательства правого заметим, что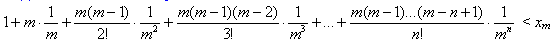 
при m > n. Переходя к пределу при m → ∞, получаем 
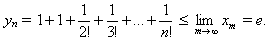б) Из а) следует, что 0 <rn 
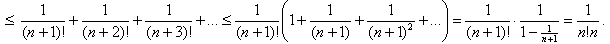в) Предположим, что e = m/n, где m и n – натуральные числа. Тогда 
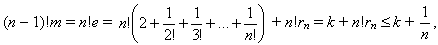где – k – целое число. Противоречие, так как (n – 1)!m – целое число, а k + n!·rn не целое.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет