Задача
Теорема Эйлера. Пусть m ≥ 1 и (a, m) = 1. Тогда aφ(m) ≡ 1 (mod m).
Докажите теорему Эйлера с помощью малой теоремы Ферма
а) в случае, когда m = pn;
б) в общем случае.
Решение
а) φ(pn) = (p – 1)pn–1. Согласно малой теореме Ферма ap–1 = 1 + kp. Следовательно,
...,
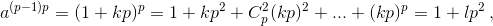
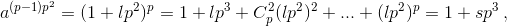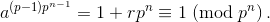б) Пусть 
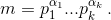Как известно, 
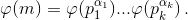Согласно а)
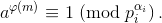Поскольку числа 
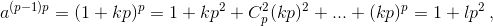взаимно просты,
aφ(m) ≡ 1 (mod m).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет