Задача
p – простое число. Сколько существует способов раскрасить вершины правильного p-угольника в a цветов? (Раскраски, которые можно совместить поворотом, считаются одинаковыми.)
Решение
Забудем временно про совмещение раскрасок поворотами. Тогда p вершин можно раскрасить ap способами (см. задачу 160348). Среди этих раскрасок есть a одноцветных. Каждая из оставшихся совмещается с p раскрасками (считая исходную). Поэтому различных неодноцветных раскрасок в p раз меньше: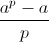 
.
Ответ
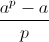способов.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет