Задача
Малая теорема Ферма. Пусть p – простое число и p не делит a. Тогда ap–1 ≡ 1 (mod p).
Докажите теорему Ферма, разлагая (1 + 1 + ... + 1)p посредством полиномиальной теоремы (см. задачу 160400).
Решение
Запишем a в виде суммы a единиц. Заметим, что все коэффициенты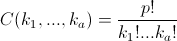 
в полиномиальной теореме кратны p, если все ki отличны от нуля (см. задачу 160668). Поэтому ap ≡ (1 + 1 +...+ 1)p ≡ 1 + 1 + … + 1 = a (mod p). Так как a и p взаимно просты, отсюда следует, что
ap–1 ≡ 1 (mod p).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет