Поскольку  2¹² ≡ 1 (mod 13),  то наименьшая степень n, при которой  2ⁿ ≡ 1 (mod 13),  – делитель числа 12. Но ни 2⁴, ни 2⁶ (а тем более 2² и 2³) не сравнимы с 1 по модулю 13. Значит, числа 2⁰, 2¹, 2², ..., 2¹¹ составляют приведённую систему вычетов по модулю 13.

  Следовательно,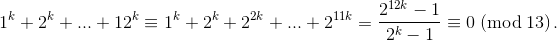  

Ответ задачи отсутствует