Задача
Пусть a1, a2, ... – такая последовательность ненулевых чисел, что (am, an) = a(m, n) (m, n ≥ 1).Докажите, что все обобщенные биномиальные коэффициенты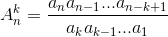 
являются целыми числами.
Решение
Число (ak, an–k) = a(k, n–k) = a(k,n) = (ak, an) является делителем числа an. Поэтому уравнение xak + yan–k = an имеет решение в целых числах (см. задачу 160489).
Если (un,k, vn,k) – одно из этих решений, то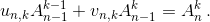 
Поскольку числа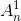 
и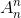 
– целые, отсюда следует, что и все числа 
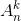– целые.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет