Задача
| 1 | ||||||||||||||
| 1 | 1 | |||||||||||||
| 1 | 1 | 1 | ||||||||||||
| 1 | 2 | 2 | 1 | |||||||||||
| 1 | 3 | 6 | 3 | 1 | ||||||||||
| 1 | 5 | 15 | 15 | 5 | 1 | |||||||||
| 1 | 8 | 40 | 60 | 40 | 8 | 1 | ||||||||
| 1 | 13 | 104 | 260 | 260 | 104 | 13 | 1 |
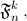определяемых равенством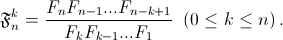
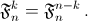б) Найдите формулу, которая выражает коэффициент 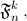через 
и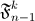 
(аналогичную равенству б) из задачи 160413). в) Объясните, почему все фибоначчиевы коэффициенты являются целыми числами.
Решение
б) Согласно задаче 160566 Fn = Fk+(n–k) = Fk–1Fn–k + FkFn–k+1. Отсюда
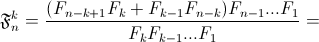
Согласно той же задаче Fn=Fk+1+(n–k–1)=FkFn–k–1+Fk+1Fn–k. Отсюда аналогично получаем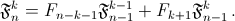 
Ответ
б)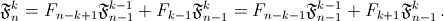 
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет