Задача
Решите в целых числах уравнения: а) x² – xy – y² = 1; б) x² – xy – y² = –1.
Решение
а) Заметим, что при подстановке пары (F2n+1, F2n) в уравнение, мы приходим к частному случаю тождества Кассини: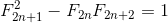 
(см. задачу 160564).
Покажем, что у исходного уравнения нет других решений. Рассмотрим, например, только натуральные решения. Нетрудно проверить, что тогда
y < x ≤ 2y. Кроме того, каждая пара решений (x, y) порождает целую цепочку решений по правилу ... → (x – y, 2y – x) → (x, y) → (2x + y, x + y) → ...
При движении по этой цепочке влево числа в парах уменьшаются: 0 < x – y < x, 0 < 2y – x < y.
Поэтому на некотором шаге получится пара, в которой y = 0, x = 1, то есть пара (F1, F0). Но эта пара порождает цепочку
... → (F1, F0) → (F3, F2) → ... → (F2n+1, F2n) → ... Значит, исходная пара должна иметь вид (x, y) = (F2n+1, F2n) = (xn, yn).
Ответ
а) ± (F2n+1, F2n), n ∈ Z; б) ± (F2n, F2n–1), n ∈ Z.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь