Задача
Докажите, что число 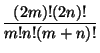 (m, n ≥ 0) целое.
(m, n ≥ 0) целое.
Решение
Лемма. [a] + [b] + [a + b] ≤ [2a] + [2b].
Доказательство. Рассмотрим два случая.
1) {a} + {b} < 1. Тогда [a + b] = [a] + [b] и [a] + [b] + [a + b] = 2[a] + 2[b] ≤ [2a] + [2b].
2) {a} + {b} ≥ 1. Тогда хотя бы одно из чисел {a}, {b} (например, {b}) не меньше ½. Поэтому [2b] = 2[b] + 1 и
[a] + [b] + [a + b] = [a] + [b] + [a] + [b] + 1 = 2[a] + 2[b] + 1 = [2a] + [2b].
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет