Задача
Пусть p – простое число и представление числа n в p-ичной системе имеет вид: n = akpk + ak–1pk–1 + ... + a1p1 + a0.
Найдите формулу, выражающую показатель αp, с которым это число p входит в каноническое разложение n!, через n, p, и коэффициенты ak.
Решение
По формуле Лежандра (см. задачу 160553)
αp = (akpk–1 + ... + a1) + (akpk–2 + ... + a2) + ... + ak = ak(pk–1 + ... + p + 1) + ... + a1 = 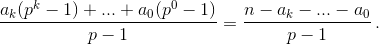
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет