а) По формуле из задачи 160537  σ(320) = σ(2³·3²·5) = 15·13·6 = 3·390 > 3·320.   б) Пусть p₁, p₂, p₃, ... – возрастающая последовательность всех простых чисел.

  Согласно задаче 134918 найдётся такое m, что  1 + ½ + … + ¹/_m > 100.

  Пусть k и α таковы, что каждое число от 2 до m раскладывается в произведение простых чисел, не превосходящих p_k, в степенях, не превосходящих α. Возьмём  n = (p₁...p_k)^α.  Тогда 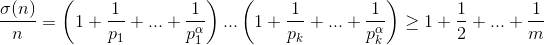  > 100  (при раскрытии скобок получатся все числа 1, ½, ..., ¹/_m  и некоторые другие.

Может.