Задача
а) Из точкиOпроведены касательныеOPиOQк эллипсу с фокусамиF1иF2. Докажите, что
$\displaystyle \angle$POQ = $\displaystyle \pi$ - $\displaystyle {\textstyle\frac{1}{2}}$($\displaystyle \angle$PF1O + $\displaystyle \angle$PF2O).
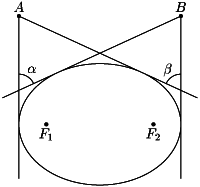
б) ОтрезокABвиден из фокусовF1иF2под углами$\varphi_{1}^{}$и$\varphi_{2}^{}$, соответственно. Докажите, что$\varphi_{1}^{}$ + $\varphi_{2}^{}$ = α + β (рис.).
Решение
а) Пусть$\angle$PF1Q= 2$\alpha$,$\angle$PF2Q= 2$\beta$,$\angle$POF1=p,$\angle$F1OF2=q. Согласно задаче 31.013
$\displaystyle \angle$PF1O = $\displaystyle \alpha$, $\displaystyle \angle$PF2O = $\displaystyle \beta$, $\displaystyle \angle$F2OQ = p;
из последнего равенства следует, что$\angle$POQ= 2p+q.
ОтрезкиPF1иPF2образуют равные углы с касательнойPO,
поэтому
$\displaystyle \alpha$ + p = $\displaystyle \angle$F2PO = $\displaystyle \pi$ - $\displaystyle \beta$ - (p + q),
т. е.$\angle$POQ= 2p+q=$\pi$- ($\alpha$+$\beta$) =$\pi$-${\dfrac{1}{2}}$($\angle$PF1Q+$\angle$PF2Q).
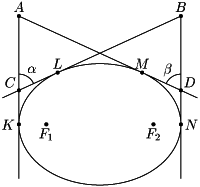
б) Введем такие обозначения
точек касания, как на рис.
Согласно задаче а)| $\displaystyle \alpha$ | = $\displaystyle {\textstyle\frac{1}{2}}$($\displaystyle \angle$KF1L + $\displaystyle \angle$KF2L), | |
| $\displaystyle \beta$ | = $\displaystyle {\textstyle\frac{1}{2}}$($\displaystyle \angle$MF1N + $\displaystyle \angle$MF2N). |
ЛучиF1AиF2Bявляются биссектрисами угловKF1MиLF2Nсоответственно, поэтому
$\displaystyle \varphi_{1}^{}$ = $\displaystyle \angle$AF1B = $\displaystyle {\textstyle\frac{1}{2}}$($\displaystyle \angle$KF1L + $\displaystyle \angle$MF1N).
Аналогично
$\displaystyle \varphi_{2}^{}$ = $\displaystyle \angle$AF2B = $\displaystyle {\textstyle\frac{1}{2}}$($\displaystyle \angle$KF2L + $\displaystyle \angle$MF2N).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет