Сделав проективное преобразование с исключительной прямой, параллельной lи проходящей через точку пересечения прямыхPP₁и QQ₁, а затем аффинное преобразование, которое образы прямых lи PP₁делает перпендикулярными, мы можем считать, что прямыеPP₁и QQ₁перпендикулярны прямой l, а наша задача заключается в том, чтобы доказать, что прямаяRR₁тоже перпендикулярна l(точки P₁,Q₁,R₁останутся серединами соответствующих отрезков, поскольку эти отрезки параллельны исключительной прямой; см. задачу 30.14, б)). ОтрезокPP₁является медианой и высотой, а значит, и биссектрисой в треугольнике, образованном прямыми l,ABи CD. Аналогично,QQ₁ — биссектриса в треугольнике, образованном прямыми l,ACи BD. Из этого и из того, чтоPP₁|QQ₁, следует, что$\angle$BAC=$\angle$BDC. Следовательно, четырехугольникABCDвписанный, и $\angle$ADB=$\angle$ACB. Обозначим точки, в которых lпересекает прямыеACи BD, через Mи N(рис.). Тогда угол между lи ADравен$\angle$ADB-$\angle$QNM=$\angle$ACB-$\angle$QMN, т. е. он равен углу между lи BC. Следовательно, треугольник, ограниченный прямыми l,ADи BC, равнобедренный, и отрезокRR₁, являющийся его медианой, является также его высотой, т. е. он перпендикулярен прямой l, что и требовалось доказать.

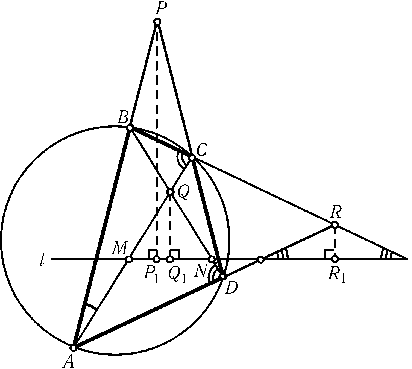
Ответ задачи отсутствует