Задачи и олимпиады по математике

Задача

На сторонахAB,BCи ACтреугольникаABCданы точки M,Nи Pсоответственно. Докажите: а) если точки M₁,N₁и P₁симметричны точкам M,Nи Pотносительно середин соответствующих сторон, тоS_MNP=S_M₁N₁P₁. б) если M₁,N₁и P₁ — такие точки сторонAC,BAи CB, чтоMM₁|BC,NN₁|CAи PP₁|AB, тоS_MNP=S_M₁N₁P₁.

Решение

а) Поскольку любой треугольник аффинным преобразованием переводится в правильный и при этом середины сторон переходят в середины сторон, центрально симметричные точки — в центрально симметричные, а равновеликие треугольники — в равновеликие треугольники (задача 29.11), то будем считать, что треугольникABCравносторонний со стороной a. Обозначим длины отрезковAM,BN,CPчерез p,q,rсоответственно. Тогда

$\begin{multline*} S_{ABC}-S_{MNP}=S_{AMP}+S_{BMN}+ S_{CNP}=\\ =\sin 60^{\circ}(p(a-r)+q(a-p)+r(a-q))/2=\sin 60^{\circ} (a(p+q+r)-(pq+qr+rp))/2. \end{multline*}$

Аналогично

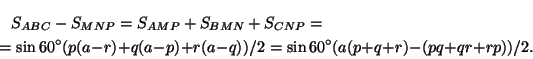
$\begin{multline*} S_{ABC}-S_{M_1N_1P_1}= \\ =\sin 60^{\circ}(r(a-p)+p(a-q)+q(a-r))/2=\sin 60^{\circ}(a(p+q+r)- (pq+qr+rp))/2. \end{multline*}$

б) Как и в предыдущей задаче, будем считать, чтоABC — правильный треугольник. ПустьM₂N₂P₂ — образ треугольникаM₁N₁P₁при повороте вокруг центра треугольникаABCна120^oв направлении от Aк B(рис.). ТогдаAM₂=CM₁=BM. Аналогично,BN₂=CNи CP₂=AP, т. е. точки M₂,N₂,P₂симметричны точкам M,N,Pотносительно середин соответствующих сторон. Тем самым задача свелась к предыдущей.

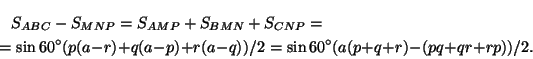
Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления