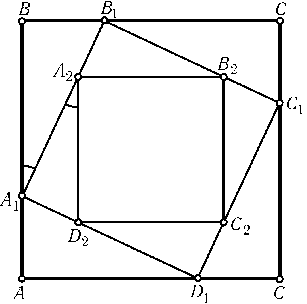
Любой параллелограммABCDаффинным преобразованием можно перевести в квадрат (для этого нужно треугольникABCперевести в равнобедренный прямоугольный треугольник). Поскольку в задаче идет речь только о параллельности прямых и об отношениях отрезков, лежащих на одной прямой, можно считать, чтоABCD — квадрат. Рассмотрим поворот на90^o, переводящийABCDв себя. При этом повороте четырехугольникиA₁B₁C₁D₁и A₂B₂C₂D₂тоже переходят в себя, следовательно, они тоже являются квадратами. При этомtgBA₁B₁=BB₁:BA₁=A₁D₂:A₁A₂=tgA₁A₂D₂, т. е.AB|A₂D₂(рис.).

Ответ задачи отсутствует