Задача
Через каждую вершину треугольника проведены две прямые, делящие противоположную сторону треугольника на три равные части. Докажите, что диагонали, соединяющие противоположные вершины шестиугольника, образованного этими прямыми, пересекаются в одной точке.
Решение
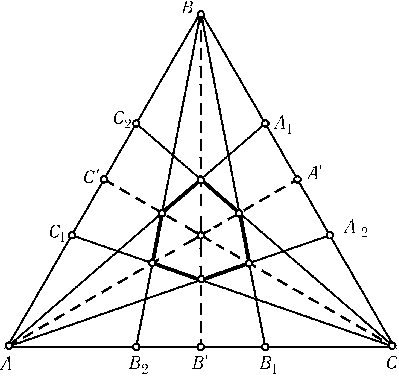
Поскольку аффинным преобразованием любой треугольник переводится в правильный (задача 29.6, б)) и при этом сохраняются отношения длин параллельных отрезков (задача 29.5), достаточно доказать утверждение задачи для правильного треугольникаABC. Пусть точки A1,A2,B1,B2,C1,C2делят стороны треугольника на равные части, а A',B',C' — середины сторон (рис.). При симметрии относительноAA'прямаяBB1перейдет в CC2, а прямаяBB2 — в CC1. Поскольку симметричные прямые пересекаются на оси симметрии,AA'содержит диагональ рассматриваемого шестиугольника. Аналогично оставшиеся диагонали лежат наBB'и CC'. Ясно, что медианыAA',BB',CC'пересекаются в одной точке.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь