Задача
Каждая из шести окружностей касается четырех из оставшихся пяти (рис.). Докажите, что для любой пары несоприкасающихся окружностей (из этих шести) их радиусы и расстояние между центрами связаны соотношениемd2=r12+r22±6r1r2(к плюск — если окружности не лежат одна внутри другой, к минуск — в противном случае).
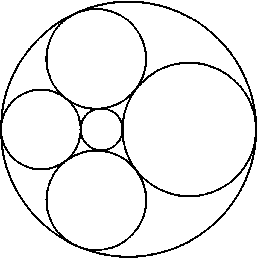
Решение
Пусть R1и R2 — какая-либо пара несоприкасающихся окружностей. Оставшиеся четыре окружности образуют цепочку, поэтому по предыдущей задаче окружности S'и S'', касающиеся R1и R2в точках их пересечения с линией центров, пересекаются под прямым углом (рис.). Если R2лежит внутри R1, то радиусы r'и r''окружностей S'и S''равны(r1+r2+d)/2 и (r1+r2-d)/2, а расстояние между их центрамиd'= 2r1-r1-r2=r1-r2. Угол между S'и S''равен углу между их радиусами, проведенными в точку пересечения, поэтому(d')2= (r')2+ (r'')2или, после преобразований,d2=r12+r22- 6r1r2. В случае, когда R1и R2не лежат одна внутри другой, радиусы окружностей S'и S''равны(d+ (r1-r2))/2 и (d- (r1-r2))/2, а расстояние между центрамиd'=r1+r2+d- (r1' +r2') =r1+r2. В результате получаемd2=r12+r22+ 6r1r2.
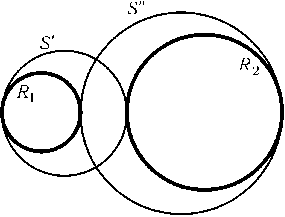
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь