Задача
Докажите, что для двух непересекающихся окружностей R1и R2цепочка из nкасающихся окружностей (см. предыдущую задачу) существует тогда и только тогда, когда угол между окружностями T1и T2, касающимися R1и R2в точках их пересечения с прямой, соединяющей центры, равен целому кратному угла360o/n(рис.).
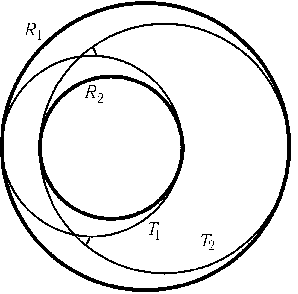
Решение
Центр инверсии, переводящей окружности R1и R2в концентрические, лежит (см. решение задачи 28.6) на линии их центров. Поэтому, сделав эту инверсию и учтя, что угол между окружностями и касание при этом сохраняется, мы сведем доказательство к случаю концентрических окружностей R1и R2с центром Oи радиусами r1и r2. Проведем окружность Sс центром Pрадиуса(r1-r2)/2, касающуюся R1изнутри и R2внешне, и две окружности S'и S''радиуса(r1+r2)/2 с центрами Aи B, касающиеся R1и R2в их точках пересечения с прямойOP(рис.). ПустьOMи ON — касательные к S, проведенные из O. Очевидно, что цепочка из nокружностей, касающихся R1и R2, существует тогда и только тогда, когда уголMONравенm360o/n(в этом случае окружности цепочки mраз обегают окружность R2). Поэтому осталось доказать, что угол между окружностями S'и S''равен$\angle$MON. Но угол между S'и S''равен углу между их радиусами, проведенными в точку пересечения C. Кроме того,$\triangle$ACO=$\triangle$PON(так какOP=r1- (r1-r2)/2 = (r1+r2)/2 =AC,PN= (r1-r2)/2 =r1- ((r1+r2)/2) =OA,$\angle$PNO=$\angle$AOC= 90o). Поэтому$\angle$ACB= 2$\angle$ACO= 2$\angle$PON=$\angle$NOM.
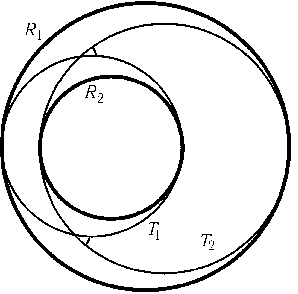
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь