Задача
Докажите, что если существует цепочка окружностейS1,S2,...,Sn, каждая из которых касается двух соседних (Snкасается Sn - 1и S1) и двух данных непересекающихся окружностей R1и R2, то таких цепочек бесконечно много. А именно, для любой окружности T1, касающейся R1и R2(одинаковым образом, если R1и R2не лежат одна в другой, внешним и внутренним образом в противном случае), существует аналогичная цепочка из nкасающихся окружностейT1,T2,...,Tn(поризм Штейнера).
Решение
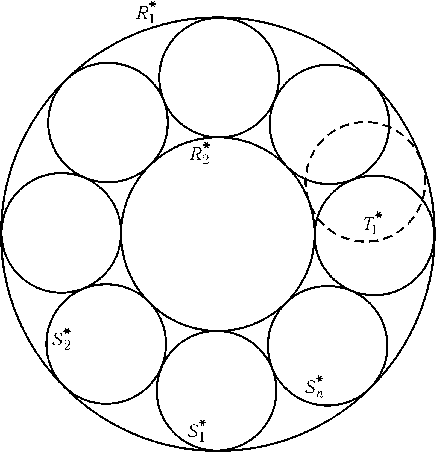
Сделаем инверсию, переводящую R1и R2в пару концентрических окружностей. Тогда окружностиS1,S2,...,Snи T1равны между собой (рис.). Повернув цепочкуS1,...,Snвокруг центра окружности R1так, чтобы S1перешла в T1*, и сделав инверсию еще раз, получим нужную цепочкуT1,T2,...,Tn.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь