Задача
Стороны выпуклого пятиугольникаABCDEпродолжили так, что образовалась пятиконечная звездаAHBKCLDMEN(рис.). Около треугольников — лучей звезды описали окружности. Докажите, что пять точек пересечения этих окружностей, отличных от A,B,C,D,E, лежат на одной окружности.
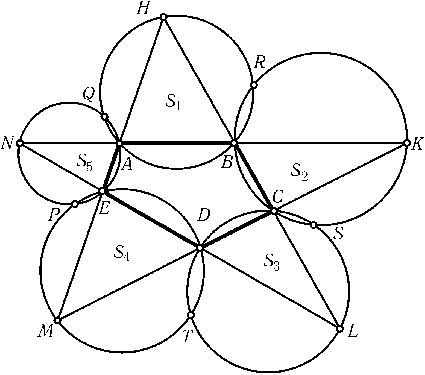
Решение
Пусть P,Q,R,S,T — точки пересечения окружностей S1,S2,S3,S4,S5, о которых говорится в условии (см. рис.). Докажем, например, что точки P,Q,R,Sлежат на одной окружности. Проведем окружность $\Sigma$, описанную около треугольникаNKD. Применяя результат задачи 2.83, а) (совпадающей с 19.45) к четырехугольникамAKDEи BNDC, получаем, что окружности S4,S5и $\Sigma$пересекаются в одной точке (в точке P) и окружности S2,S3,$\Sigma$тоже пересекаются в одной точке (в точке S). Следовательно, окружность $\Sigma$проходит через точки Pи S. Заметим теперь, что из восьми точек пересечения окружностей $\Sigma$,S1,S2,S5четыре, а именно N,A,B,Kлежат на одной прямой. Следовательно, согласно задаче 28.31оставшиеся четыре точки P,Q,R,Sлежат на одной окружности.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь