Задача
Даны четыре окружности S1,S2,S3,S4. Пусть S1и S2пересекаются в точках A1и A2,S2и S3 — в точках B1и B2,S3и S4 — в точках C1и C2,S4и S1 — в точках D1и D2(рис.). Докажите, что если точки A1,B1,C1,D1лежат на одной окружности S(или прямой), то и точки A2,B2,C2,D2лежат на одной окружности (или прямой).
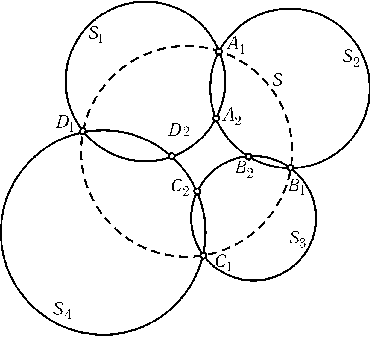
Решение
Сделаем инверсию с центром в точке A1. Тогда окружности S1,S2и S4перейдут в прямыеA2D1,B1A2и D1B1, окружности S3и S4 — в окружности S3и S4, описанные около треугольниковB2C1B1и C1D1D2(рис.). Проведем окружность через точки B2,D2,A2. Согласно задаче 2.80, а) она пройдет через точку C2пересечения окружностей S3и S4. Таким образом, точки A2,B2,C2,D2лежат на одной окружности. Следовательно, точки A2,B2,C2,D2лежат на одной окружности или прямой.
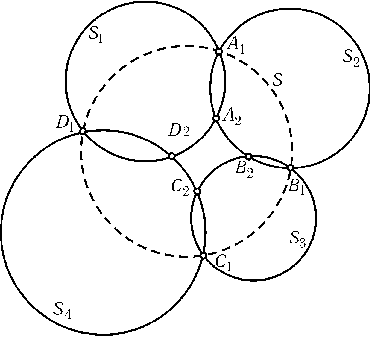
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь