Задача
ОкружностьSAпроходит через точкиAиC; окружностьSBпроходит через точкиBиC; центры обеих окружностей лежат на прямойAB. ОкружностьSкасается окружностейSAиSB, а кроме того, она касается отрезкаABв точкеC1. Докажите, чтоCC1 — биссектриса треугольникаABC.
Решение
Сделаем инверсию с центромC, при которой прямаяABпереходит в окружностьS', проходящую через точку пересечения окружностейSAиSB(отличную от точкиC). При такой инверсии окружностиSAиSBпереходят в прямые, проходящие через центрOокружностиS'(рис.). Ясно, что окружностьSкасается окружностиS'в середине дугиAB*.
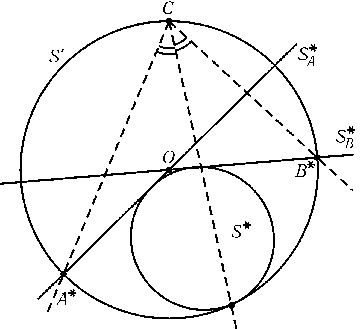
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет