Задача
В сегмент вписываются всевозможные пары пересекающихся окружностей, и для каждой пары через точки их пересечения проводится прямая. Докажите, что все эти прямые проходят через одну точку (см. задачу 3.44).
Решение
Пусть S1и S2 — окружности, вписанные в сегмент;M,N — их точки пересечения (рис.). Покажем, что прямаяMNпроходит через точку Pокружности сегмента, равноудаленную от его концов Aи B. Действительно, согласно предыдущей задаче инверсия с центром Pи степеньюPA2переводит отрезокABв дугуAB, а окружности S1и S2 — в окружности S1и S2, по-прежнему вписанные в сегмент. Но касательные к S1, проведенные из P, касаются также и S1, поэтомуS1=S1(так как обе эти окружности одинаковым образом касаются трех фиксированных прямых). АналогичноS2=S2, следовательно, точки Mи Nменяются местами при инверсии, т. е.M=Nи прямаяMNпроходит через центр инверсии.
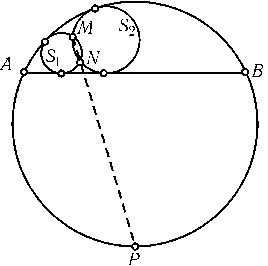
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь