Пусть C — вершина данного угла. При инверсии с центром в точке AпрямаяCBперейдет в окружность S, а окружности S₁и S₂ — в окружность S₁с центром O₁, касающуюся Sв точке B, и прямую l, параллельнуюCA, касающуюся S₁в точке X(рис.). Проведем в окружности SрадиусOD$\perp$CA. Точки O,Bи O₁лежат на одной прямой, aOD|O₁X. Поэтому$\angle$OBD= 90^o-$\angle$DOB/2 = 90^o- ($\angle$XO₁B/2) =$\angle$O₁BX, следовательно, точка Xлежит на прямойDB. Еще раз применив инверсию, получим, что искомое множество точек касания — это дугаABокружности, проходящей через точки A,Bи D.

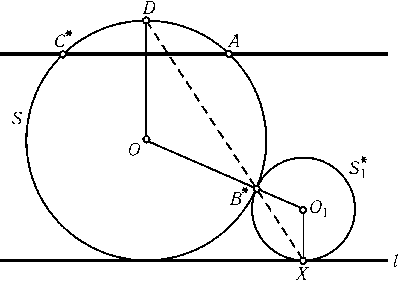
Ответ задачи отсутствует