ПустьABCD— исходный квадрат,A₁B₁C₁D₁— квадрат с тем же центром, стороны которого параллельны сторонам исходного квадрата и имеют вдвое большую длину. Для определённости будем считать, что сторона исходного квадрата равна 2. Тогда периметр квадратаA₁B₁C₁D₁равен 16. Поэтому достаточно доказать, что длина части периметра квадратаA₁B₁C₁D₁, высекаемой приложенным квадратом, не может быть меньше 2. Рассмотрим два возможных варианта расположения квадратаA₁B₁C₁D₁и приложенного квадрата.

1. Ни одна вершина квадратаA₁B₁C₁D₁не попадает внутрь приложенного квадрата. В этом случае рассматриваемая часть периметра является отрезкомPQ. Если внутри квадратаA₁B₁C₁D₁лежит только одна вершина приложенного квадрата (та, которая примыкает к исходному квадрату), то длина отрезкаPQравнаtg$\alpha$+${\frac{1}{{\rm tg}\alpha}}$$\ge$2; здесь$\alpha$— угол между стороной исходного квадрата и стороной приложенного квадрата. Если внутри квадратаA₁B₁C₁D₁лежат две вершины приложенного квадрата, то отрезокPQявляется гипотенузой прямоугольного треугольника с катетом 2.
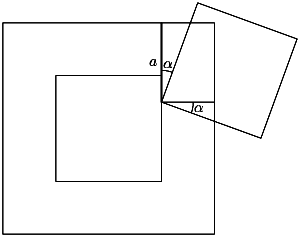
2. Одна вершина квадратаA₁B₁C₁D₁попадает внутрь приложенного квадрата. Тогда длина рассматриваемой части периметра равнаa+tg$\alpha$+ 1 -atg$\alpha$(рис.). Требуется доказать, чтоa+tg$\alpha$+ 1 -atg$\alpha$$\ge$2, т.е.(a- 1)tg$\alpha$$\le$(a- 1). Ноa$\ge$1 иtg$\alpha$$\le$1.

Ответ задачи отсутствует