Задача
Имеется неограниченное количество плиток в форме многоугольникаM. Будем говорить, что из этих плиток можно сложить паркет, если ими можно покрыть круг сколь угодно большого радиуса так, чтобы не было ни просветов, ни перекрытий. а) Докажите, что еслиM — выпуклыйn-угольник, гдеn$\ge$7, то паркет сложить нельзя. б) Приведите пример такого выпуклого пятиугольника с попарно непараллельными сторонами, что паркет сложить можно.
Решение
а) Предположим, что кругKрадиусаRпокрыт паркетом, состоящим из одинаковых выпуклыхn-угольников. Рассмотрим все точки, лежащие внутри кругаKи являющиеся вершинамиn-угольников. Эти точки бывают двух типов: точки 1-го типа лежат на сторонах другихn-угольников и сумма углов, сходящихся в них, равна180o; в точках 2-го типа сходятся углы, сумма которых равна360o. Пустьpиq — количества точек 1-го и 2-го типа соответственно. В каждой точке 1-го типа сходится не менее двух угловn-угольников, а в каждой точке 2-го типа — не менее трех углов. Поэтому,2p+ 3q$\le$2nL1, гдеL1 — количествоn-угольников, пересекающихся сK. Суммы углов, сходящихся в точках 1-го и 2-го типа равны180oи360oсоответственно. Поэтомуp+ 2q$\ge$(n- 2)L2, гдеL2 — количествоn-угольников, лежащих внутриK. Сложив неравенства4p+ 6q$\le$4nL1и-3p- 6q$\le$6L2- 3nL2, получимp$\le$6L2-n(4L1- 3L2), т. е.p/L2$\le$6 -n(4L1/L2- 3). Так как$\lim_{R \to \infty}^{}$L1/L2= 1, то$\lim_{R \to \infty}^{}$p/L2= 6 -n. Значит, если из данных выпуклыхn-угольников можно сложить паркет, то 6 -n$\ge$0, т. е.n$\le$6. б) См. рис.
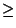
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь