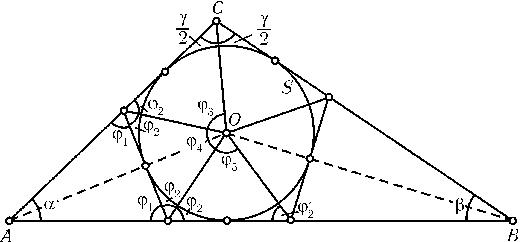
$\angle$ACB> 90^oиO — центр вписанной окружностиSтреугольникаABC. Проведем кSкасательные через точки пересеченияSс отрезкамиOAиOBи обозначим получившиеся углы, как показано на рис. Последовательно вычисляя углы, получаем, что$\phi_{1}^{}$= ($\pi$-$\alpha$)/2 <$\pi$/2,$\phi_{2}^{}$= ($\pi$-$\phi_{1}^{}$)/2 = ($\pi$+$\alpha$)/4 <$\pi$/2 (аналогично= ($\pi$+$\beta$)/4),$\phi_{3}^{}$=$\pi$-$\phi_{2}^{}$-$\gamma$/2 = 3$\pi$/4 -$\alpha$/4 -$\gamma$/2 <$\pi$/2 + ($\pi$/4 -$\gamma$/2) <$\pi$/2,$\phi_{4}^{}$=$\pi$- 2$\phi_{2}^{}$= ($\pi$-$\alpha$)/2 <$\pi$/2 и$\phi_{5}^{}$=$\pi$-$\phi_{2}^{}$-=$\pi$/2 -$\alpha$/4 -$\beta$/4 <$\pi$/2. Аналогично доказывается, что и все остальные углы семи треугольников, изображенных на рис., меньше90^o.

Ответ задачи отсутствует