Разрезание треугольника на подобные неравные треугольники — олимпиадна

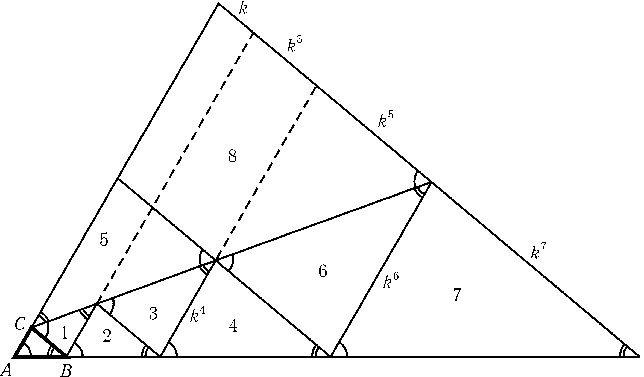
а) Можно считать, чтоBC/AC=k> 1. Приложим к треугольникуABCтреугольники 1, 2, 3, 4 и 5 (см. рис.). Может оказаться, что треугольники 4 и 5 равны, т. е.k+k³=k⁴. В этом случае дополним конструкцию треугольниками 6 и 7, а треугольник 5 заменим треугольником 8. Тогда треугольники 7 и 8 не равны, т. е.k⁶ ≠ k+k³+k⁵. В самом деле, так какk+k³=k⁴, тоk⁶=k²(k+k³) =k³+k⁵<k+k³+k⁵.

б) Предположим, что правильный треугольник разрезан на неравные правильные треугольники. Стороны двух треугольников разбиения не могут совпадать. Будем рассматривать только стороны треугольников разбиения, лежащие внутри (не на границе) исходного треугольника; пустьN — число таких сторон. Возникает три типа вершин треугольников разбиения (см. рис.). Из каждой вершины 1-го, 2-го и 3-го типа выходит соответственно 4, 12 и 6 сторон. Пустьn₁,n₂иn₃ — количества точек 1-го, 2-го и 3-го типа. ТогдаN= (4n₁+ 12n₂+ 6n₃)/2 = 2n₁+ 6n₂+ 3n₃. Каждой точке 3-го типа можно сопоставить 3 стороны (на рис. это стороныAB,OPиOQ). Легко проверить, что каждая сторона будет соответствовать хотя бы одной точке 3-го типа. Следовательно,N$\le$3n₃, а значит,2n₁+ 6n₂$\le$0. В частности,n₁= 0, т. е. разбиение состоит лишь из исходного треугольника.

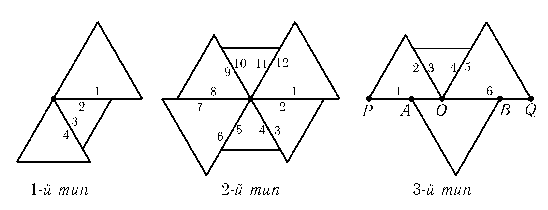
Ответ задачи отсутствует