Задача
Из 16 плиток размером 1×3 и одной плитки 1×1 сложили квадрат со стороной 7. Докажите, что плитка 1×1 лежит в центре квадрата или примыкает к его границе.
Решение
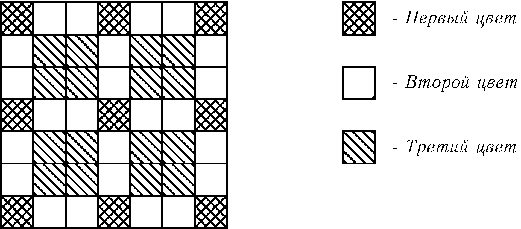
Разобьем полученный квадрат на клетки размером 1×1 и раскрасим их в три цвета, как показано на рис. Легко проверить, что плитки 1×3 можно разбить на два типа: плитка 1-го типа накрывает одну клетку 1-го цвета и две клетки 2-го цвета, а плитка 2-го типа накрывает одну клетку 2-го цвета и две клетки 3-го цвета. Предположим, что все клетки 1-го цвета накрыты плитками 1×3. Тогда плиток 1-го типа 9, а плиток 2-го типа 7. Следовательно, они накрывают9 . 2 + 7 = 25 клеток 2-го цвета и 7 . 2 = 14 клеток 3-го цвета. Получено противоречие, поэтому одна из клеток 1-го цвета накрыта плиткой 1×1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь