Доказательство проведем индукцией по n. Приn= 3 утверждение очевидно. Если одно из чисел $\alpha_{i}^{}$, равно $\pi$, то шаг индукции очевиден, поэтому можно считать, что все числа $\alpha_{i}^{}$отличны от $\pi$. Еслиn$\ge$4, то${\frac{1}{n}}$$\sum\limits_{i=1}^{n}$($\alpha_{i}^{}$+$\alpha_{i+1}^{}$) = 2(n- 2)$\pi$/n$\ge$$\pi$, причем равенство достигается только для четырехугольника. Значит, в любом случае, кроме параллелограмма($\alpha_{1}^{}$=$\pi$-$\alpha_{2}^{}$=$\alpha_{3}^{}$=$\pi$-$\alpha_{4}^{}$), найдутся два соседних числа, сумма которых больше $\pi$. Более того, найдутся такие числа $\alpha_{i}^{}$и $\alpha_{i+1}^{}$, что$\pi$<$\alpha_{i}^{}$+$\alpha_{i+1}^{}$< 3$\pi$. В самом деле, если все данные числа меньше $\pi$, то можно взять вышеуказанную пару чисел; если же$\alpha_{j}^{}$>$\pi$, то можно взять такие числа $\alpha_{i}^{}$и $\alpha_{i+1}^{}$, что$\alpha_{i}^{}$<$\pi$и $\alpha_{i+1}^{}$>$\pi$. Пусть$\alpha_{i}^{}$=$\alpha_{i}^{}$+$\alpha_{i+1}^{}$-$\pi$. Тогда0 <$\alpha_{i}^{}$< 2$\pi$, поэтому по предположению индукции существует (n- 1)-угольник Mс углами$\alpha_{1}^{}$,...,$\alpha_{i-1}^{}$,$\alpha_{i}^{}$,$\alpha_{i+2}^{}$,...,$\alpha_{n}^{}$. Возможны три случая: 1) $\alpha_{i}^{}$<$\pi$, 2) $\alpha_{i}^{}$=$\pi$, 3) $\pi$<$\alpha_{i}^{}$< 2$\pi$. В первом случаеa_i+a_{i + 1}< 2$\pi$, поэтому одно из этих чисел, например $\alpha_{i}^{}$, меньше $\pi$. Если$\alpha_{i+1}^{}$<$\pi$, то отрежем от Mтреугольник с углами$\pi$-$\alpha_{i}^{}$,$\pi$-$\alpha_{i+1}^{}$,$\alpha_{i}^{}$(рис., а), если$\alpha_{i+1}^{}$>$\pi$, то приставим к Mтреугольник с углами$\alpha_{i}^{}$,$\alpha_{i+1}^{}$-$\pi$,$\pi$-$\alpha_{i}^{}$(рис., б). Во втором случае отрежем от Mтрапецию с основанием, лежащим на сторонеA_{i - 1}A_iA_{i + 2}(рис., в). В третьем случае$\alpha_{i}^{}$+$\alpha_{i+1}^{}$>$\pi$, поэтому одно из этих чисел, например $\alpha_{i}^{}$, больше $\pi$. Если$\alpha_{i+1}^{}$>$\pi$, то приставим к Mтреугольник с углами$\alpha_{i}^{}$-$\pi$,$\alpha_{i+1}^{}$-$\pi$,2$\pi$-$\alpha_{i}^{}$(рис., г), если$\alpha_{i+1}^{}$<$\pi$, то отрежем от Mтреугольник с углами2$\pi$-$\alpha_{i}^{}$,$\pi$-$\alpha_{i+1}^{}$и $\alpha_{i}^{*}$-$\pi$(рис., д).

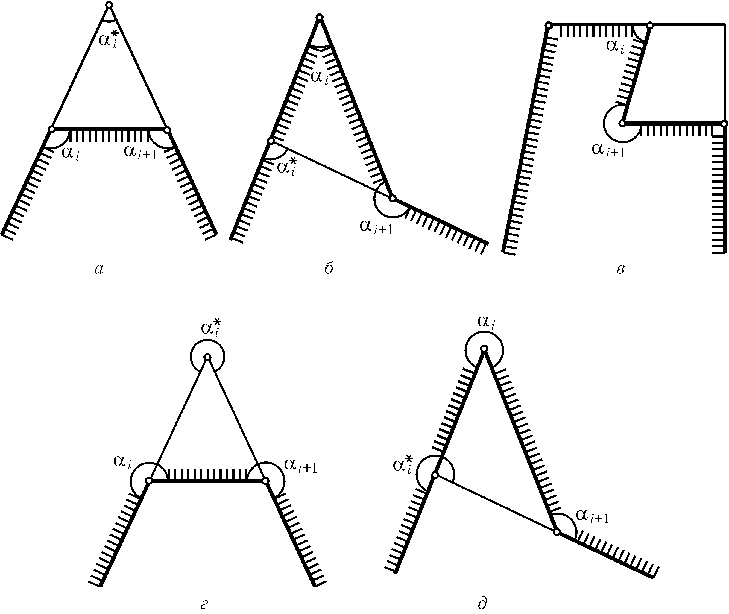
Ответ задачи отсутствует