Задача
С невыпуклым несамопересекающимся многоугольником производятся следующие операции. Если он лежит по одну сторону от прямойAB, где Aи B — несмежные вершины, то одна из частей, на которые контур многоугольника делится точками Aи B, отражается относительно середины отрезкаAB. Докажите, что после нескольких таких операций многоугольник станет выпуклым.
Решение
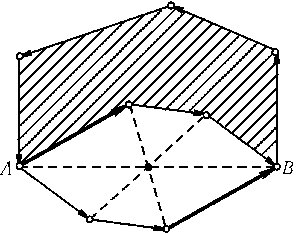
При этих операциях векторы сторон многоугольника остаются теми же самыми; изменяется только их порядок (рис.). Поэтому имеется лишь конечное число многоугольников, которые могут получиться. Кроме того, после каждой операции площадь многоугольника строго возрастает. Следовательно, процесс конечен.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет