Пусть k — число острых угловn-угольника. Тогда сумма его углов меньшеk ^. 90^o+ (n-k) ^. 360^o. С другой стороны, сумма угловn-угольника равна(n- 2) ^. 180^o(см. задачу 22.23), поэтомуk ^. 90^o+ (n-k) ^. 360^o> (n- 2) ^. 180^o, т. е. 3k< 2n+ 4. Следовательно,k$\le$[2n/3] + 1, где через [x] обозначено наибольшее целое число, не превосходящее x. Примерыn-угольников, имеющих [2n/3] + 1 острых углов, приведены на рис.

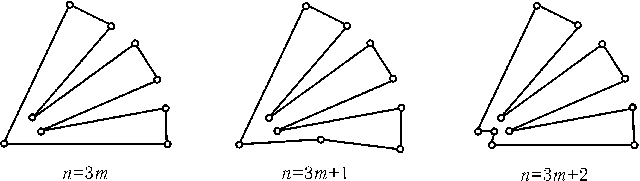
Ответ задачи отсутствует