Предположим, что существует тринадцатиугольник, у которого на любой прямой, содержащей сторону, есть еще хотя бы одна сторона. Проведем через все стороны этого тринадцатиугольника прямые. Так как у него тринадцать сторон, то на одной из них лежит нечетное число сторон, т. е. на одной прямой лежат по крайней мере три стороны. У них есть 6 вершин и через каждую вершину проходит прямая, на которой лежат по крайней мере две стороны. Поэтому всего у этого тринадцатиугольника не менее3 + 2 ^. 6 = 15 сторон, чего не может быть. Для четногоn$\ge$10 требуемый пример — контур к звездык (рис., а); идея построения примера для нечетного nпоказана на рис., б).

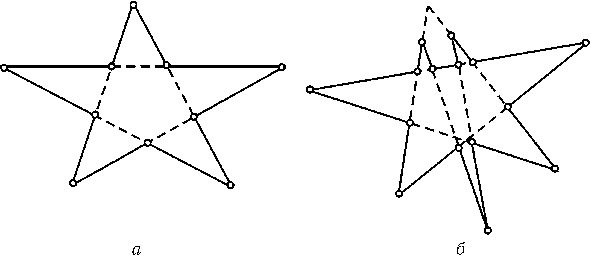
Ответ задачи отсутствует