Задача
Докажите, что сумма внешних углов любого многоугольника, прилегающих к меньшим180oвнутренним углам, не меньше360o.
Решение
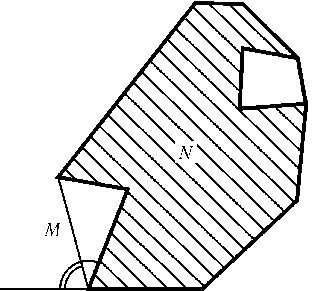
Так как у выпуклогоn-угольника все внутренние углы меньше180oи их сумма равна(n- 2) . 180o, то сумма внешних углов равна360o, т. е. в случае выпуклого многоугольника достигается равенство. Пусть теперь M — выпуклая оболочка многоугольника N. Каждый угол Mсодержит меньший180oугол N, причем угол Mможет быть только больше угла N, т. е. внешний угол Nне меньше внешнего угла M(рис.). Поэтому, даже ограничившись только углами N, примыкающими к углам M, мы уже получим не меньше360o.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет