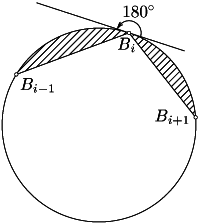
ПустьK— круг, в который вписан многоугольникB₁...B_n. Построим на каждой сторонеA_iA_{i + 1}многоугольникаA₁...A_nвнешним образом сегмент, равный сегменту, отсекаемому сторонойB_iB_{i + 1}от кругаK, и рассмотрим фигуру$\Phi$, состоящую из многоугольникаA₁...A_nи этих сегментов. Два таких сегмента могут пересечься только если$\angle$A_{i - 1}A_iA_{i + 1}-$\angle$B_{i - 1}B_iB_{i + 1}> 180^o(рис.), а этого не может быть, поскольку многоугольникA₁...A_nвыпуклый. ПоэтомуS_{$\scriptstyle \Phi$}=S_A1...An+SиS_K=S_B1...Bn+S, гдеS— сумма площадей сегментов. Ясно также, чтоP_{$\scriptstyle \Phi$}=P_K. Следовательно, согласно изопериметрическому неравенствуS_K$\ge$S_{$\scriptstyle \Phi$}, т.е.S_B1...Bn$\ge$S_A1...An, причём равенство достигается только в том случае, когда$\Phi$— круг, а многоугольникA₁...A_nвписанный.

Ответ задачи отсутствует