Для всех подобных многоугольников отношение площади к квадрату периметра постоянно. Поэтому достаточно доказать, что среди всех выпуклых многоугольников с данными углами отношение площади к квадрату периметра будет наибольшим для описанного многоугольника. а) Рассмотрим сначала случай, когда четырёхугольникABCD— параллелограмм с заданным углом α. Если его стороны равныaиb, то отношение площади к квадрату периметра равно

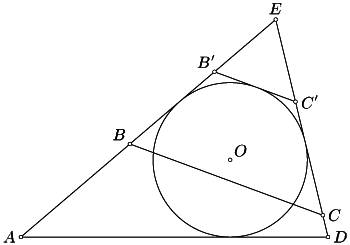
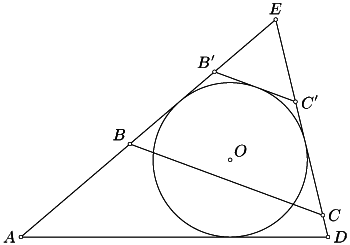
причём равенство достигается только приa=b, т.е. в случае, когдаABCD— ромб. Ромб является описанным четырёхугольником. Будем теперь считать, чтоABCD— не параллелограмм. Тогда продолжения двух его сторон пересекаются. Пусть для определённости лучиABиDCпересекаются в точкеE. Проведём прямуюB'C'||BC, касающуюся вписанной в треугольникAEDокружности (рис.; точкиB'иC'лежат на сторонахAEиDE). Пустьr— радиус вписанной окружности треугольникаAED,O-- её центр. Тогдагдеq= (EB'+EC'-B'C')/2. Поэтомугдеp— полупериметр треугольникаAED,k=EB/EB'. Вычислим теперь периметрABCD. Сумма периметровABCDиEBCравна сумме периметраAEDи 2BC, поэтому периметрABCDравен2p- (EB+EC-BC) = 2p- 2kq. Следовательно, отношение площади четырёхугольникаABCDк квадрату его периметра равно${\frac{pr-k^2qr}{4(p-kq)^2}}$. Для описанного четырёхугольникаAB'C'D'такое отношение равно${\frac{pr-qr}{4(p-q)^2}}$, поскольку для негоk= 1. Остаётся доказать неравенство${\frac{pr-k^2qr}{4(p-kq)^2}}$$\le$${\frac{pr-qr}{4(p-q)^2}}$, т.е.${\frac{p-k^2q}{4(p-kq)^2}}$$\le$${\frac{1}{p-q}}$(сократить наp-qможно, потому чтоp>q). Неравенство(p-k²q)(p-q)$\le$(p-kq)²верно, поскольку его можно привести к виду-pq(1 -k)²$\le$0. Равенство достигается только приk= 1, т.е. в случае, когда четырёхугольникABCDописанный. б) Доказательство проведём индукцией поn. Дляn= 4 утверждение доказано в задаче а). Доказательство шага индукции начнём с доказательства того, что приn$\ge$5 у любогоn-угольника есть сторона, для которой сумма прилегающих к ней углов больше180^o. Действительно, сумма всех пар углов, прилегающих к сторонам, равна удвоенной сумме угловn-угольника, поэтому сумма углов, прилегающих к одной из сторон, не меньше(n- 2) ^. 360^o/n$\ge$360^{o .} 3/5 > 180^o. Пусть для определённости сумма углов при вершинахA₁иA₂больше180^o. Тогда лучиA_nA₁иA₃A₂пересекаются в точкеB(рис.). Рассмотрим также вспомогательный описанныйn-угольникA₁'...A_n' со сторонами, параллельными сторонамA₁...A_n. Обозначим точку пересечения лучейA_n'A₁' иA₃'A₂' черезB'. Для облегчения вычислений будем считать, что периметры (n- 1)-угольниковBA₃A₄...A_{n - 1}иB'A₃'A₄'...A_{n - 1}' одинаковы и равныP(этого можно добиться переходом к подобным многоугольникам). Пустьr— радиус вписанной окружности многоугольникаA₁'...A_n'. Тогда площадь многоугольникаB'A₃'A₄'...A_{n - 1}' равнаrP/2. По предположению индукции площадь (n- 1)-угольникаBA₃A₄...A_{n - 1}не больше площадиB'A₃'A₄'...A_{n - 1}', т.е. она равна$\alpha$rP/2, где$\alpha$$\le$1, причём$\alpha$= 1 только в случае, когда многоугольникB'A₃'A₄'...A_{n - 1}' описанный. Пусть площадь треугольникаA₁'A₂'B'равнаS, а коэффициент подобия треугольниковA₁A₂BиA₁'A₂'B'равенk. Тогда площадь треугольникаA₁A₂Bравнаk²S. Ясно, чтогдеq=A₁'B'+A₂'B'-A₁'A₂'. Поэтому площади многоугольниковA₁...A_nиA₁'...A_n' равныr(P-q)/2 иr($\alpha$P-k²q)/2, а их периметры равныP-qиP-kq. Остаётся доказать, чтопричём равенство достигается только при$\alpha$= 1 иk= 1 (если$\alpha$= 1, то многоугольникиBA₃A₄...A_{n - 1}иB'A₃'A₄'...A_{n - 1}' равны, а если при этом ещё иk= 1, то$\triangle$A₁A₂B=$\triangle$A₁'A₂'B', т.е. многоугольникиA₁...A_nиA₁'...A_n' равны). Несложные вычисления показывают, что неравенство(P-q)($\alpha$P-k²q)$\le$(P-kq)²эквивалентно неравенствуПоследнее неравенство справедливо, причём равенство достигается только при α = 1.

Ответ задачи отсутствует