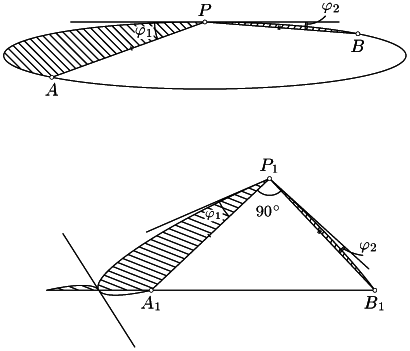
Рассмотрим хордуAB, делящую пополам периметр фигуры$\Phi$. ЕслиABделит фигуру$\Phi$на две части разной площади, то согласно задаче 22.BIs11существует фигура$\Phi{^\prime}$, которая имеет тот же периметр, что и$\Phi$, но большую площадь. Поэтому будем считать, что хордаABделит фигуру$\Phi$на две части равной площади. На границе$\Phi$есть точкаP, для которой$\angle$APB$\ne$90^o, поскольку иначе$\Phi$— круг с диаметромAB. Займёмся построением требуемой фигуры$\Phi{^\prime}$. Построим прямоугольный треугольникP₁A₁B₁с катетамиP₁A₁=PAиP₁B₁=PBи приставим к его катетам сегменты, отсекаемые хордамиPAиPB(рис.). Если такой сегмент будет теперь разрезан прямойA₁B₁, то, отразив одну из его частей относительно точки пересечения границы с прямойA₁B₁, получим фигуру, лежащую по одну сторону от прямойA₁B₁. Сегменты, прилегающие к катетамA₁P₁иP₁B₁, не могут пересечься, поскольку угол между опорными прямыми в точкеP₁равен90^o+$\varphi_{1}^{}$+$\varphi_{2}^{}$= 90^o+ (180^o-$\angle$APB) < 270^o. Пусть$\Phi{^\prime}$— фигура, состоящая из построенной нами фигуры и фигуры, симметричной ей относительно прямойA₁B₁. Тогда$\Phi{^\prime}$имеет тот же периметр, что и$\Phi$, но большую площадь, так как

Замечание. Этими рассуждениями мы не доказали, что среди всех фигур данного периметра наибольшую площадь имеет круг. Мы не доказывали, что среди всех фигур данного периметра есть фигура наибольшей площади.

Ответ задачи отсутствует