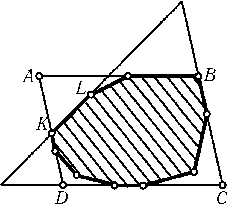
Если многоугольник не треугольник и не параллелограмм, то у него найдутся две непараллельные несоседние стороны. Продолжив их до пересечения, получим новый многоугольник, содержащий исходный и имеющий меньшее число сторон. После нескольких таких операций получим треугольник или параллелограмм. Если получится треугольник, то все доказано; поэтому будем считать, что получился параллелограммABCD. На каждой его стороне лежит сторона исходного многоугольника, и одна из его вершин, например A, не принадлежит исходному многоугольнику (рис.). Пусть K — ближайшая к Aвершина многоугольника, лежащая наAD, aKL — сторона, не лежащая наAD. Тогда многоугольник заключен внутри треугольника, образованного прямымиKL,BCи CD.

Ответ задачи отсутствует