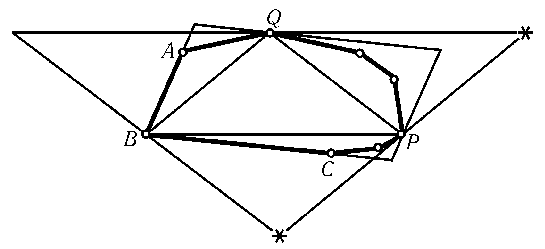
Рассмотрим выпуклую оболочку данных точек. Возможны два случая.

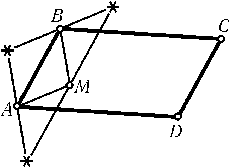
1. Выпуклая оболочка является параллелограммомABCD. Если точка Mлежит внутри параллелограммаABCD, то вершины всех трех параллелограммов с вершинами A,Bи Mлежат внеABCD(рис.). Значит, в этом случае, кроме точек A,B,Cи D, никаких других точек быть не может.

2. Выпуклая оболочка не является параллелограммом. ПустьABи BC — стороны выпуклой оболочки. Проведем опорные прямые, параллельныеABи BC. Пусть эти опорные прямые проходят через вершины Pи Q. Тогда вершины всех трех параллелограммов с вершинами B,Pи Qлежат вне выпуклой оболочки (рис.). Они даже лежат вне параллелограмма, образованного опорными прямыми, кроме того случая, когда Pи Qявляются вершинами этого параллелограмма. В этом случае его четвертая вершина не принадлежит выпуклой оболочке, так как та не является параллелограммом.

Ответ задачи отсутствует