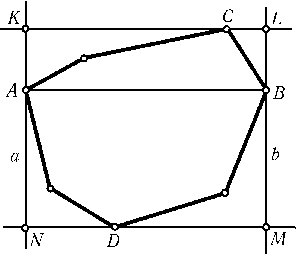
ПустьAB — наибольшая диагональ (или сторона) многоугольника. Проведем через точки Aи Bпрямые aи b, перпендикулярные прямойAB. Если X — вершина многоугольника, тоAX$\le$ABи XB$\le$AB, поэтому многоугольник находится внутри полосы, образованной прямыми aи b. Проведем опорные прямые многоугольника, параллельныеAB. Пусть эти прямые проходят через вершины Cи Dи вместе с прямыми aи bобразуют прямоугольникKLMN(рис.). ТогдаS_KLMN= 2S_ABC+ 2S_ABD= 2S_ACBD. Так как четырехугольникACBDсодержится в исходном многоугольнике, площадь которого равна 1, тоS_KLMN$\le$2.

Ответ задачи отсутствует