Задача
Пусть O — точка пересечения диагоналей выпуклого четырехугольникаABCD. Докажите, что если периметры треугольниковABO,BCO,CDOи DAOравны, тоABCD — ромб.
Решение
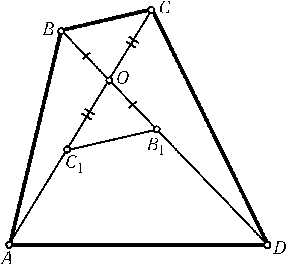
Для определенности можно считать, чтоAO$\ge$COи DO$\ge$BO. Пусть точки B1и C1симметричны точкам Bи Cотносительно точки O(рис.). Так как треугольникB1OC1лежит внутри треугольникаAOD, тоPAOD$\ge$PB1OC1=PBOC, причем равенство достигается, только еслиB1=DиC1=A(см. задачу 9.27, б)). Следовательно,ABCD — параллелограмм. ПоэтомуAB-BC=PABO-PBCO= 0, т. е.ABCD — ромб.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет