Задача
На плоскости дано конечное число попарно непараллельных прямых, причем через точку пересечения любых двух из них проходит еще одна из данных прямых. Докажите, что все эти прямые проходят через одну точку.
Решение
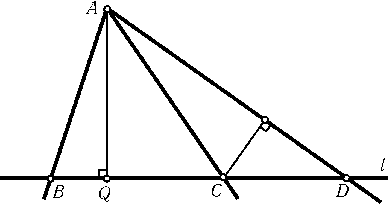
Предположим, что не все прямые проходят через одну точку. Рассмотрим точки пересечения прямых и выберем наименьшее ненулевое расстояние от этих точек до данных прямых. Пусть наименьшим будет расстояние от точки Aдо прямой l. Через точку Aпроходят по крайней мере три данные прямые. Пусть они пересекают прямую lв точках B,Cи D. Опустим из точки AперпендикулярAQна прямую l. Две из точек B,Cи Dлежат по одну сторону от точки Q, например Cи D. Пусть для определенностиCQ<DQ(рис.). Тогда расстояние от точки Cдо прямойADменьше, чем расстояние от точки Aдо прямой l, что противоречит выбору Aи l.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь