Задача
Пусть l1,l2и l3 — соответственные прямые подобных фигур F1,F2и F3, пересекающиеся в точке W. а) Докажите, что точка Wлежит на окружности подобия фигур F1,F2и F3. б) Пусть J1,J2и J3 — точки пересечения прямых l1,l2и l3с окружностью подобия, отличные от точки W. Докажите, что эти точки зависят только от фигур F1,F2и F3и не зависят от выбора прямых l1,l2и l3.
Решение
а) Пусть l1',l2' и l3' — соответственные прямые фигур F1,F2и F3, причем li'|li; эти прямые образуют треугольникP1P2P3. При поворотной гомотетии с центром O3, переводящей F1в F2, прямые l1и l1' переходят в l2и l2', поэтому при гомотетии с центром O3, переводящей прямую l1в l1', прямая l2переходит в l2'. Следовательно, прямаяP3O3проходит через точку W. Аналогично прямыеP1O1и P2O2проходят через точку W, а значит, точка Wлежит на окружности подобия фигур F1,F2и F3(см. задачу 19.49, б)). б) Отношение расстояний от точки O1до прямых l2' и l3' равно коэффициенту поворотной гомотетии, переводящей F2в F3, а угол P1треугольникаP1P2P3равен углу ее поворота. Поэтому$\angle$(O1P1,P1P2) зависит лишь от фигур F2и F3. А так как$\angle$(O1W,WJ3) =$\angle$(O1P1,P1P2), то дугаO1J3фиксирована (рис.), а значит, точка J3фиксирована. Аналогично доказывается, что точки J1и J2фиксированы.
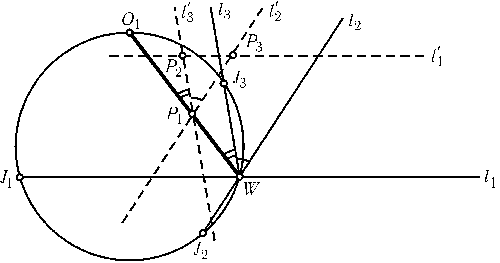
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь