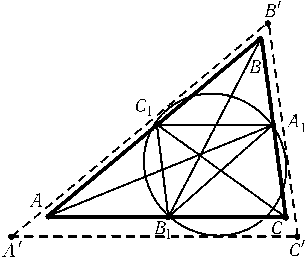
Пусть A₁,B₁и C₁ — середины сторонBC,ACи ABсоответственно. При гомотетии с центром в точке пересечения медиан треугольника и коэффициентом гомотетии -1/2 описанная окружность SтреугольникаABCпереходит в описанную окружность S₁треугольникаA₁B₁C₁. Так как окружность S₁пересекает все стороны треугольникаABC, то можно построить треугольникA'B'C'со сторонами, параллельными сторонам треугольникаABC, для которого S₁будет вписанной окружностью (рис.). Пусть rи r' — радиусы вписанных окружностей треугольниковABCи A'B'C';Rи R₁ — радиусы окружностей Sи S₁. Ясно, чтоr$\le$r'=R₁=R/2. Равенство достигается, если треугольникиA'B'C'и ABCсовпадают, т. е. S₁ — вписанная окружность треугольникаABC. В этом случаеAB₁=AC₁, поэтомуAB=AC. АналогичноAB=BC.

Ответ задачи отсутствует