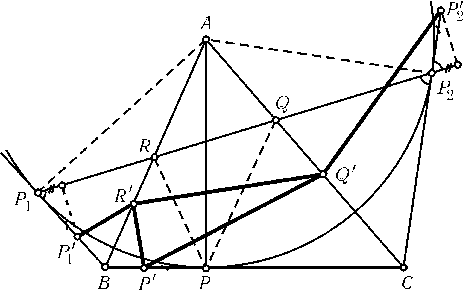
ПустьPQR — треугольник, образованный основаниями высот треугольникаABC,P'Q'R' — любой другой треугольник, вписанный в треугольникABC. Пусть, далее, точки P₁и P₂(соответственно,P₁' и P₂') симметричны точке P(соответственно P') относительно прямыхABи AC(рис.). Точки Qи Rлежат на отрезкеP₁P₂(см. задачу 1.57), поэтому периметр треугольникаPQRравен длине отрезкаP₁P₂. А периметр треугольникаP'Q'R'равен длине ломанойP₁'R'Q'P₂', т. е. он не меньше длины отрезкаP₁'P₂'. Остается заметить, что(P₁'P₂')²=P₁P₂²+ 4d², где d — расстояние от точки P₁' до прямойP₁P₂.

Ответ задачи отсутствует