Задача
Угол, изготовленный из прозрачного материала, двигают так, что две непересекающиеся окружности касаются его сторон внутренним образом. Докажите, что на нем можно отметить точку, которая описывает дугу окружности.
Решение
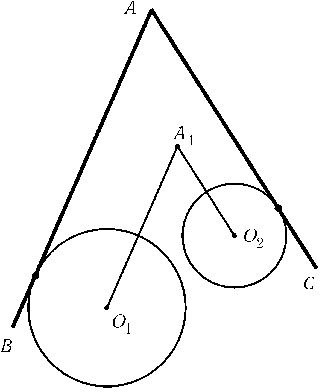
Пусть сторонаABуглаBACкасается окружности радиуса r1с центром O1, сторонаACкасается окружности радиуса r2с центром O2. Перенесем прямуюABпараллельно внутрь углаBACна расстояние r1, прямуюAC — на расстояние r2. Пусть A1 — точка пересечения перенесенных прямых (рис.). Тогда$\angle$O1A1O2=$\angle$BAC. Постоянный уголO1A1O2опирается на неподвижный отрезокO1O2, поэтому точка A1описывает дугу окружности.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет