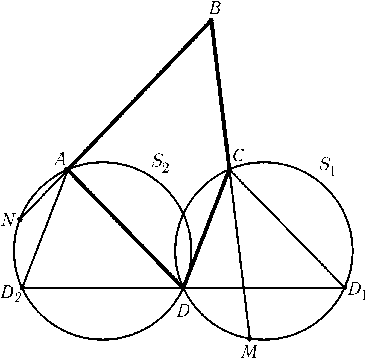
Предположим, что искомый четырехугольникABCDпостроен. Пусть D₁и D₂ — образы точки Dпри переносах на векторы$\overrightarrow{AC}$и $\overrightarrow{CA}$соответственно. Опишем вокруг треугольниковDCD₁и DAD₂окружности S₁и S₂. Обозначим точки пересечения прямыхBCи BAс окружностями S₁и S₂через Mи N(рис.). Ясно, что$\angle$DCD₁=$\angle$DAD₂=$\angle$D,$\angle$DCM= 180^o-$\angle$Cи $\angle$DAN= 180^o-$\angle$A. Из этого вытекает следующее построение. На произвольной прямой lберем точку Dи строим на lточки D₁и D₂так, чтоDD₁=DD₂=AC. Фиксируем одну из полуплоскостей П, заданных прямой l, и будем считать, что точка Bлежит в этой полуплоскости. Построим окружность S₁, из точек которой, лежащих в П, отрезокDD₁виден под углом D. Аналогично строим окружность S₂. Построим точку Mна S₁так, чтобы из всех точек части окружности, лежащей в П, отрезокDMбыл виден под углом180^o-$\angle$C. Аналогично строим точку N. ОтрезокMNвиден из точки Bпод углом B, т. е. Bявляется точкой пересечения окружности с центром DрадиусаDBи дуги окружности, из которой отрезокMNвиден под углом B(и она лежит в полуплоскости П). Точки Cи Aявляются точками пересечения прямыхBMи BNс окружностями S₁и S₂.

Ответ задачи отсутствует