Задача
Даны непересекающиеся хордыABи CDокружности. Постройте точку Xокружности так, чтобы хордыAXи BXвысекали на хордеCDотрезокEF, имеющий данную длину a.
Решение
Предположим, что точка Xпостроена. Перенесем точку Aна вектор$\overrightarrow{EF}$, т. е. построим точку A', для которой$\overrightarrow{EF}$=![]() . Это построение можно сделать, так как вектор$\overrightarrow{EF}$известен: его длина равна aи он параллеленCD.
ПосколькуAX|A'F, то$\angle$A'FB=$\angle$AXB, поэтому уголA'FBизвестен. Таким образом, точка Fлежит на пересечении двух фигур:
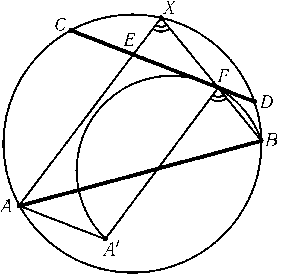
отрезкаCDи дуги окружности, из которой отрезокA'Bвиден под угломAXB(рис.).
. Это построение можно сделать, так как вектор$\overrightarrow{EF}$известен: его длина равна aи он параллеленCD.
ПосколькуAX|A'F, то$\angle$A'FB=$\angle$AXB, поэтому уголA'FBизвестен. Таким образом, точка Fлежит на пересечении двух фигур:
отрезкаCDи дуги окружности, из которой отрезокA'Bвиден под угломAXB(рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет