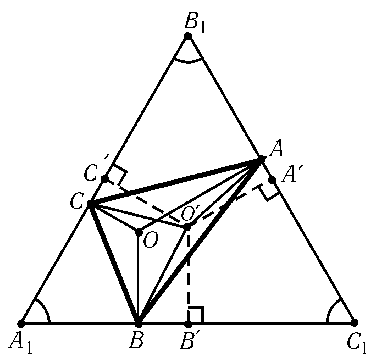
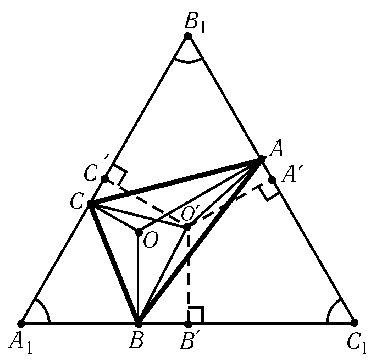
Предположим сначала, что все углы треугольникаABCменьше120^o. Тогда внутри его существует точка O, из которой все стороны видны под углом120^o. Проведем через вершины A,Bи Cпрямые, перпендикулярные отрезкамOA,OBи OC. Эти прямые образуют правильный треугольникA₁B₁C₁(рис.). Пусть O' — любая точка, лежащая внутри треугольникаABCи отличная от точки O. Докажем, что тогдаO'A+O'B+O'C>OA+OB+OC, т. е.O — искомая точка. Пусть A',B'и C' — основания перпендикуляров, опущенных из точки O'на стороныB₁C₁,C₁A₁иA₁B₁,a — длина стороны правильного треугольникаA₁B₁C₁. ТогдаO'A'+O'B'+O'C'= 2(S_O'B1C1+S_O'A1B1+S_O'A1C1)/a= 2S_A1B1C1/a=OA+OB+OC. Так как наклонная длиннее перпендикуляра, тоO'A+OB+O'C>O'A'+O'B'+O'C'=OA+OB+OC.

Пусть теперь один из углов треугольникаABC, например угол C, больше или равен120^o. Проведем через точки Aи BперпендикулярыB₁C₁иC₁A₁к отрезкамCAиCB, а через точку C — прямуюA₁B₁, перпендикулярную биссектрисе углаACB(рис.). Так как$\angle$AC₁B= 180^o-$\angle$ACB< 60^o, тоB₁C₁>A₁B₁. Пусть O' — любая точка, лежащая внутри треугольникаA₁B₁C₁. ПосколькуB₁C₁ ^. O'A'+C₁A₁ ^. O'B'+A₁B₁ ^. O'C'= 2S_A1B1C1, то(O'A'+O'B'+O'C') ^. B₁C₁= 2S_A1B1C1+ (B₁C₁-A₁B₁) ^. O'C'. Так какB₁C₁>A₁B₁, то суммаO'A'+O'B'+O'C'минимальна для точек, лежащих на сторонеB₁A₁. Ясно также, чтоO'A+O'B+O'C$\ge$O'A'+O'B'+O'C'. Следовательно, искомой точкой является вершина C.

Ответ задачи отсутствует